The goal of fcirt is to estimate forced choice models using Bayesian method. Specifically, the Multi-Unidimensional Pairwise Preference (MUPP) model is estimated using the R package rstan that utilizes the Hamiltonian Monte Carlo sampling algorithm. Below are some important features of the fcirt package:
You can install fcirt from CRAN:
install.packages("fcirt")You can install the development version of fcirt from GitHub:
devtools::install_github("Naidantu/fcirt")This is a basic example which shows you how to prepare data, fit the model, extract and plot results:
library(fcirt)
## basic example code
## Step 1: Input data
# 1.1 Response data in wide format. If the first statement is preferred, the data should be coded as 1, otherwise it should be coded as 2.
fcirt.Data <- c(1,2,2,1,1,1,1,1,NA,1,2,1,1,2,1,1,2,2,NA,2,2,2,1,1,1,2,1,1,1,1,2,1,1,1,2,1,1,2,1,1)
fcirt.Data <- matrix(fcirt.Data,nrow = 10)
fcirt.Data
#> [,1] [,2] [,3] [,4]
#> [1,] 1 2 2 2
#> [2,] 2 1 2 1
#> [3,] 2 1 1 1
#> [4,] 1 2 1 1
#> [5,] 1 1 1 2
#> [6,] 1 1 2 1
#> [7,] 1 2 1 1
#> [8,] 1 2 1 2
#> [9,] NA NA 1 1
#> [10,] 1 2 1 1
# 1.2 A two-column data matrix: the first column is the statement number for statement s; the second column is the statement number for statement t.
pairmap <- c(1,3,5,7,2,4,6,8)
pairmap <- matrix(pairmap,ncol = 2)
pairmap
#> [,1] [,2]
#> [1,] 1 2
#> [2,] 3 4
#> [3,] 5 6
#> [4,] 7 8
# 1.3 A column vector mapping each statement to each trait.
ind <- c(1,2,1,2,1,2,2,1)
# 1.4 A three-column matrix containing initial values for the three statement parameters (alpha, delta, tau) respectively. If using the direct MUPP estimation approach, 1 and -1 for alphas and taus are recommended and -1 or 1 for deltas are recommended depending on the signs of the statements. If using the two-step estimation approach, pre-estimated statement parameters are used as the initial values. The R package **bmggum** (Tu et al., 2021) can be used to estimate statement parameters for the two-step approach.
ParInits <- c(1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, -1, 1, 1, -1, -1, -1, -1, -1, -1, -1, -1)
ParInits <- matrix(ParInits, ncol = 3)
ParInits
#> [,1] [,2] [,3]
#> [1,] 1 1 -1
#> [2,] 1 -1 -1
#> [3,] 1 1 -1
#> [4,] 1 1 -1
#> [5,] 1 1 -1
#> [6,] 1 -1 -1
#> [7,] 1 1 -1
#> [8,] 1 1 -1
## Step 2: Fit the MUPP model
mod <- fcirt(fcirt.Data=fcirt.Data, pairmap=pairmap, ind=ind, ParInits=ParInits, iter=1000)
## Step 3: Extract the estimated results
# 3.1 Extract the theta estimates
theta <- extract(x=mod, pars='theta')
# Turn the theta estimates into p*trait matrix where p equals sample size and trait equals the number of latent traits
theta <- theta[,1]
# nrow=trait
theta <- matrix(theta, nrow=2)
theta <- t(theta)
# theta estimates in p*trait matrix format
theta
#> [,1] [,2]
#> [1,] -0.008846518 -0.020839511
#> [2,] -0.010909129 0.014170047
#> [3,] 0.039271194 -0.029510418
#> [4,] 0.053650150 -0.003515530
#> [5,] -0.014835090 -0.038893088
#> [6,] -0.029746453 0.003989843
#> [7,] 0.046490462 0.007792688
#> [8,] 0.027869493 -0.032391257
#> [9,] 0.027951501 -0.011935207
#> [10,] 0.062773955 -0.012719476
# 3.2 Extract the tau estimates
tau <- extract(x=mod, pars='tau')
tau <- tau[,1]
tau
#> tau[1] tau[2] tau[3] tau[4] tau[5] tau[6] tau[7]
#> -2.0540455 -0.9805878 -1.2825280 -1.4354192 -1.7621815 -1.0457171 -1.8182223
#> tau[8]
#> -1.0445483
#3.3 Extract the estimates of the correlations among dimensions
cor <- extract(x=mod, pars='cor')
## Step 4: Plottings
# 4.1 Obtain the density plots for alpha
bayesplot(x=mod, pars='alpha', plot='density', inc_warmup=FALSE)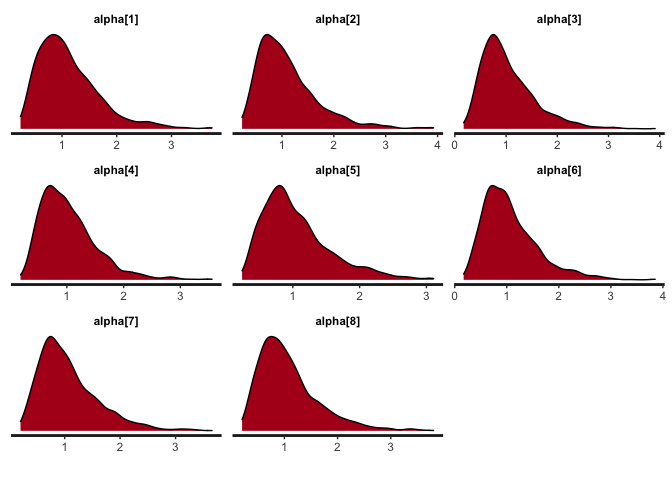
# 4.2 Obtain the trace plots for alpha
bayesplot(x=mod, pars='alpha', plot='trace', inc_warmup=FALSE)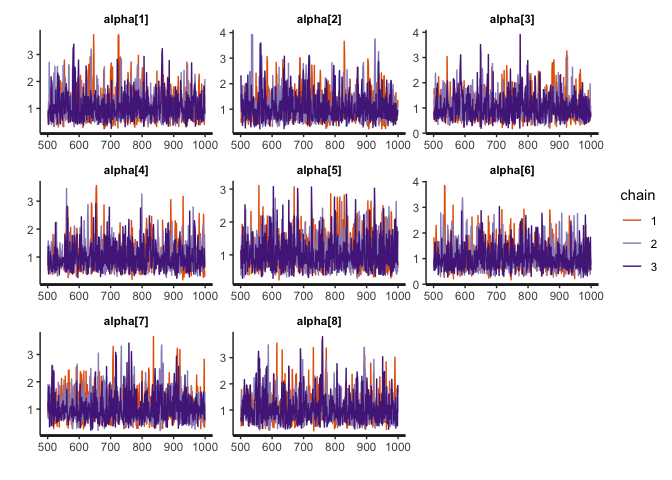
## Step 5: Item information
# 5.1 Obtain item information for item 1-3
OII <- information(x=mod, approach="direct", information="item", items=1:3)
OII
#> [1] 0.3915412 0.4035285 0.3920269
# 5.2 Obtain test information
OTI <- information(x=mod, approach="direct", information="test")
OTI
#> [1] 1.577941